Nadeln beim Hindernislauf
Dünne Nanofasern in paradoxer Zickzack-Bewegung
Das Verhalten einfacher Gase wie Sauerstoff oder Helium ist sehr gut verstanden, seit die Physiker Rudolf Clausius, James Clerk Maxwell und Ludwig Boltzmann Mitte des 19. Jahrhunderts die kinetische Gastheorie entwickelten. Völlig anders aber stellt sich die Situation für Dichte Systeme aus sehr langen, dünnen Fasern dar, wie sie aktuell in der Nanotechnologie untersucht werden. Wenn sich eine derartige Faser dreht, stößt sie sofort mit vielen anderen Fasern zusammen, und es kommt zu einer starken gegenseitigen Behinderung - ähnlich wie in Flüssigkeiten.
Die Wissenschaftler Dr. Felix Höfling, Professor Erwin Frey und Privatdozent Dr. Thomas Franosch vom Arnold-Sommerfeld-Zentrum für Theoretische Physik der Ludwig-Maximilians-Universität (LMU) fanden nun aber einen unerwarteten neuen Effekt: Die Diffusion der Fasern wird trotz der starken Behinderungen nicht langsamer, vielmehr erhöht sich ihre Geschwindigkeit dramatisch. „Anhand eines einfachen Modells und umfangreicher Computersimulationen konnten wir beobachten, dass sich die Fasern über 100mal schneller bewegen als erwartet“, berichtet Franosch.
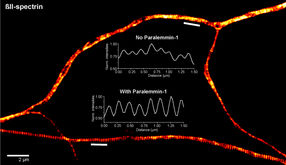
Dieser Effekt lässt sich auf eine weiträumige Zickzack-Bewegung der Fasern zurückführen, die Spuren der Bewegung ähneln den Bahnen eines Schlittschuhläufers. Physikalisch formuliert: Ein Axiom der kinetischen Gastheorie ist die Hypothese des molekularen Chaos, von Boltzmann "Stoßzahlansatz" genannt. Demnach ist die Bewegung der Moleküle nach einem Stoß unabhängig von ihrer vorherigen Bewegung. Dadurch aber wird eine statistische Beschreibung mit Hilfe zufälliger Prozesse möglich, und die makroskopischen Eigenschaften sind von den mikroskopischen Details der Stöße unabhängig.
Für lang gestreckte Fasern, so ein Ergebnis der Arbeit, ist diese Hypothese nur noch teilweise gültig. Obwohl die Bewegung nicht deterministisch vorhersagbar ist, wird sie nicht vollständig zufällig. Die Fasern laufen vielmehr lange Strecken geradeaus und ändern nur sehr langsam ihre Orientierung. Dadurch werden mikroskopische Details verstärkt und in der makroskopischen Zickzack-Bewegung sichtbar.
Wie eine Faser an den „Spitzen“ ihrer Zickzack-Bewegung genau abgebremst wird und schließlich rückwärts läuft, führt zur Erklärung für die erhöhte Diffusionskonstante. Eine sorgfältige Analyse zeigt, dass die Diffusionskonstante mit der Dichte der Nadeln über ein Fraktal zusammenhängt. Obwohl die Wissenschaftler die grundlegenden Mechanismen für die erhöhte Diffusion erklären konnten, gibt es Hinweise, dass für eine präzisere Beschreibung die Mathematik der Fraktale, des Chaos und der quasi-periodischen Orbits eine wesentliche Rolle spielt, was weitere Grundlagenforschung anregen wird.
Originalveröffentlichung: Felix Höfling, Erwin Frey, and Thomas Franosch; “Enhanced Diffusion of a Needle in a Planar Array of Point Obstacles”, Physical Review Letters, 19. September 2008
Weitere News aus dem Ressort Wissenschaft
Holen Sie sich die Analytik- und Labortechnik-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für Analytik und Labortechnik bringt Sie jeden Dienstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
